全期望定理公式推导

字数统计: 1.2k阅读时长: 4 min

 2025/07/13 

引言

最近推导强化学习的Bellman equation，在化解第二项Future Reward项时，需要用到全期望定理，秉承费曼学习法的理念，这里从两个方面对全期望定理公式进行介绍。首先，我们以一个简单的例子从感性上理解该公式，然后再从数学的角度对其进行较为严谨的推导。

全期望定理公式

假设$B_1, B_2, …, B_n$ 是一组互不相容的事件，并且形成样本空间的一个分割；
$C$是一个确定事件，且 $p(C) > 0$；
$A$是一个随机变量。

则有：
$$E[A | C] = \sum_{i=1}^{n} p(B_i | C) E[A |B_i, C] $$
上述公式即为全期望定理公式。

对公式的感性理解

用大白话来说就是：我想知道，在已知发生了$C$ 的条件下，随机变量$A$的的平均值是多少？那我们可以先看看，在$C$里，各个子情况$B_i$发生的概率有多少，然后在每个小情况里算一下$A$的平均值，最后加权求和就好了。

就像是：

假如我们做一个实验：

$C$表示“你进入了一所大学”
$B_1$表示“你进的是数学系”，$B_2$表示“你进的是物理系”…… (这些系把大学分成了划分)
$A$表示“你的未来收入”

那么问题是： 在你已经进入大学（B）的前提下，你的未来收入的平均值是多少？

答案就是：

你在数学系的概率 x 数学系的平均收入
你在物理系的概率 x 物理系的平均收入
…

以上加起来就是你在大学的平均收入。

Note: 不想看枯燥数学公式的同学看到这里就好了，可以跳过下面的数学证明部分。

对公式的证明

全期望定理公式的推导

下面，我们来证明全期望定理公式：$$E[A | C] = \sum_{i=1}^{n} p(B_i | C) E[A |B_i, C] $$

我们从条件概率的全概率公式（稍后我们再对该公式进行推导）：

$$
\begin{align}
p(A=a|C) = \sum_{i=1}^{n} p(A=a|B_i, C) p(B_i|C)
\end{align}
$$

出发，进行推导。

首先，对公式(1) 的左边进行加权求和，得到期望表达式：

$$
\begin{align*}
E[A | C] &= \sum_{a\in A} P(a |C)a \
\end{align*}
$$
接下来，代入公式(1) 的右边，得到：
$$\begin{align*}
E[A | C] &= \sum_{a\in A} \sum_{i=1}^{n} p(A=a|B_i, C) p(B_i|C) a \
&= \sum_{i=1}^{n} p(B_i|C) \sum_{a\in A} p(A=a|B_i, C) a \
&= \sum_{i=1}^{n} p(B_i|C) E[A | B_i, C] \
\end{align*}
$$
最终，我们得到了全期望定理公式：
$$E[A | C] = \sum_{i=1}^{n} p(B_i | C) E[A |B_i, C] $$

至此，我们从条件概率的全概率公式出发，推导出了全期望定理公式。下面我们从更一般的概念，推导条件概率的全概率公式。

条件概率的全概率公式的推导

假设$B_1, B_2, …, B_n$ 是一组互不相容的事件，并且形成样本空间的一个分割；
$C$是一个确定事件，且 $p(C) > 0$；
$A$是一个随机变量。

我们需要推导出下面的等式：
$$p(A | C) = \sum_{i=1}^{n} p(A | B_i, C) P(B_i | C)$$

推导过程：

我们从条件概率的定义出发：
$p(A | C) = \frac{p(A \cap C)}{p(C)}$，
我们希望把$p(A|C)$表达为关于$B_i$的加权和。

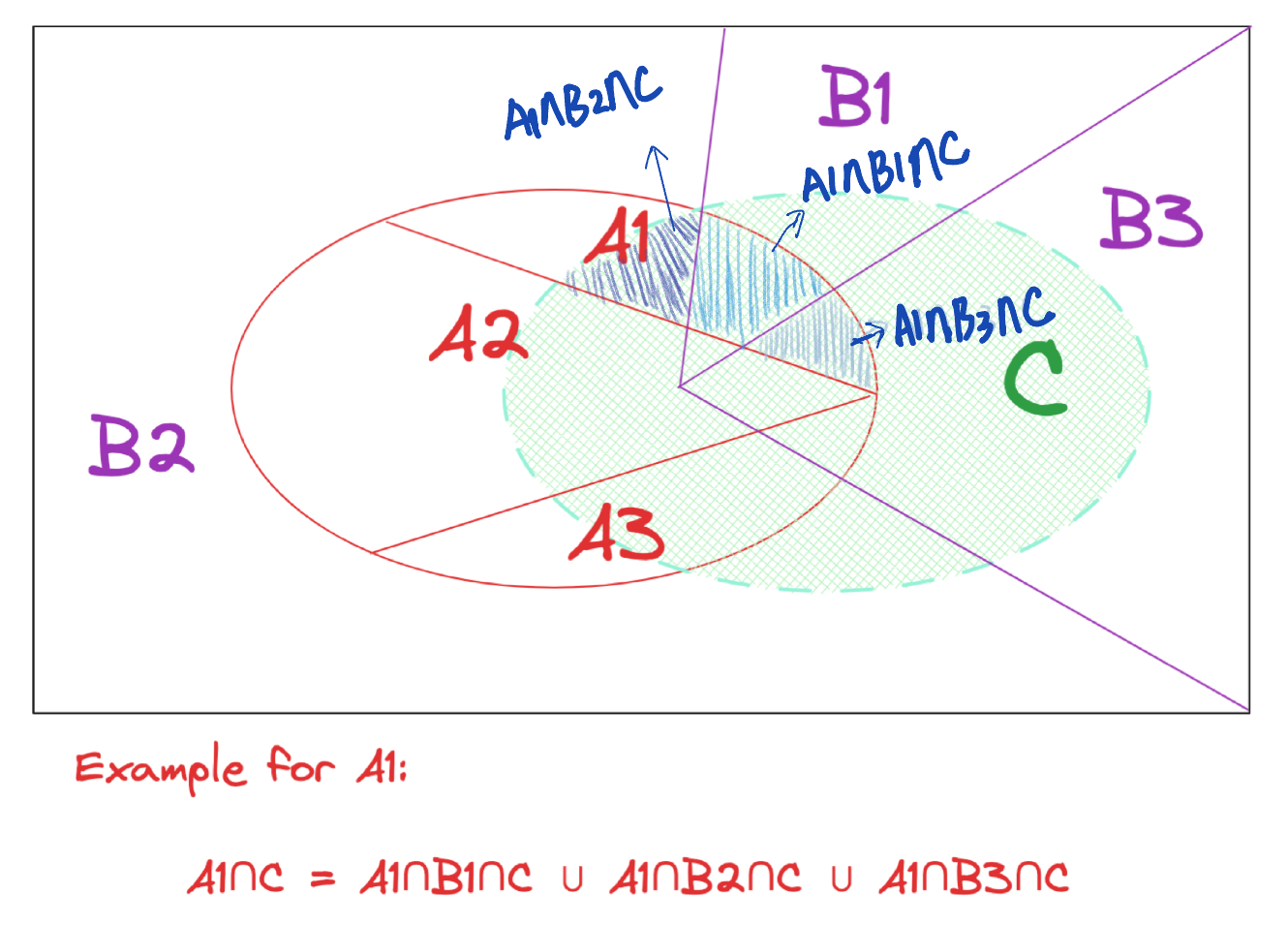
使用全概率公式计算$p(A \cap C)$：因为$B_1, B_2, …$ 是一组互不相容的事件，并形成样本空间的一个分割，所以 $A \cap C$ = $\bigcup_{i=1}^{n} (A \cap B_i \cap C)$(如图所示)，同时，这些$A \cap B_i \cap C$
两两两互不相容，因此：
$$p(A \cap C) = \sum_{i=1}^{n} p(A \cap B_i \cap C)$$
根据概率的乘法公式，我们对每一项 $p(A \cap B_i \cap C)$进行展开：
$$p(A \cap B_i \cap C) = p(A | B_i \cap C) p(B_i \cap C) $$
代入上面的公式，得到：
$$p(A \cap C) = \sum_{i=1}^{n} p(A | B_i \cap C) p(B_i \cap C)$$
将上式，代入 $p(A | C) = \frac{p(A \cap C)}{p(C)}$，得到：
$$
\begin{align*}
p(A | C) &= \frac{\sum_{i=1}^{n} p(A | B_i \cap C) p(B_i \cap C)}{p(C)} \
&= \sum_{i=1}^{n} p(A | B_i \cap C) \frac{p(B_i \cap C)}{p(C)} \
&= \sum_{i=1}^{n} p(A | B_i, C) p(B_i | C)
\end{align*}
$$
综上，我们得到了条件概率的全概率公式：
$$p(A | C) = \sum_{i=1}^{n} p(A | B_i, C) P(B_i | C)$$