变分推断
应用举例
- 文章LAD题目分析
对文本进行自动分析,然后自动从中找出topic
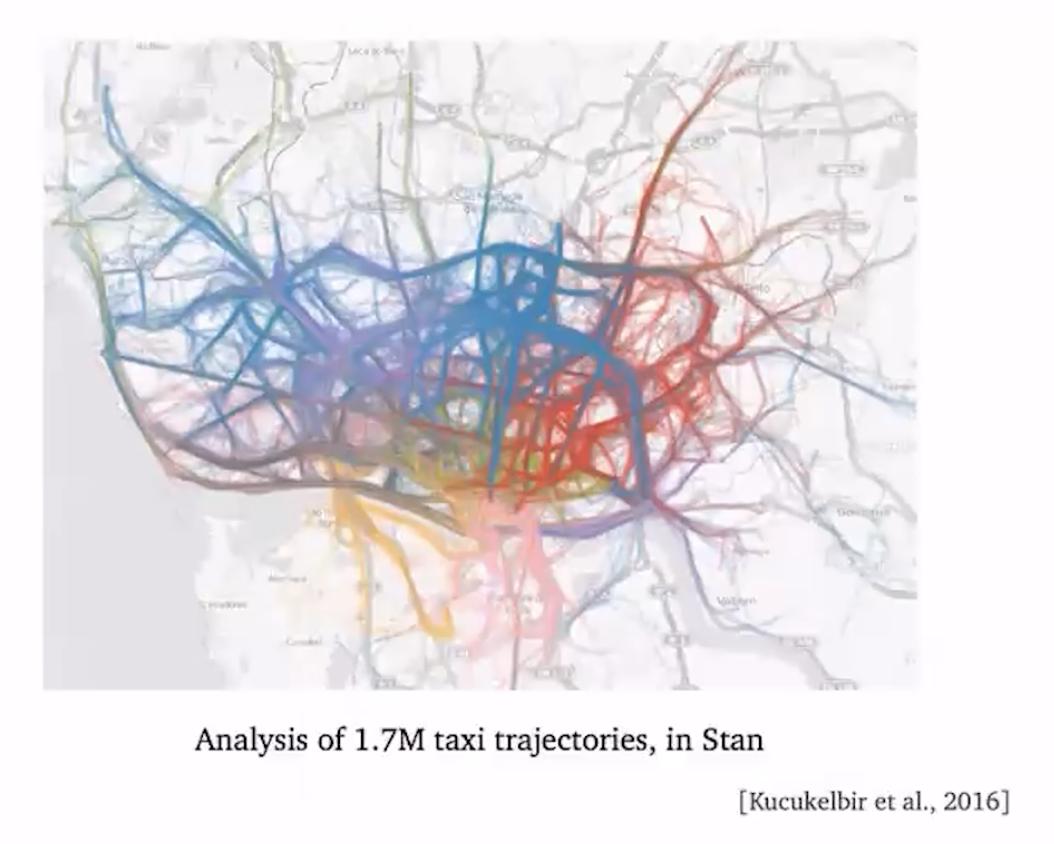
交通数据分析
美国湾区出租车数据分析,用变分推断的方法可以在一台笔记本电脑上面完成大量数据的计算
贝叶斯推断概述
目标优缺点

Roadmap

接下来主要讲解变分贝叶斯方法,变分贝叶斯方法是近似贝叶斯推断的一大类方法,变分贝叶斯方法又有很多子类,Mean-field变分推断是其中比较有代表性的一类。接下来结合讲解的方法讲三个例子:univariate Gaussian、Mixture of Gaussians和LDA
贝叶斯推断

Data是观测变量,Parameters是模型的参数,通过对观测变量$x$取值的观测,我们可以更新参数$z$, 这里$p(x) = \int_{z}^{}{p(x,z)dz}$,实际应用中$z$是一个高维的分布,很难计算$p(z|x)$
近似贝叶斯推断_

直接计算$p(z|x)$复杂度很高很难,然后就有了近似计算(推断)。常用的近似计算有:MCMC方法和基于优化的方法,MCMC方法虽然精度高但是数据量大时计算很慢,基于随机梯度的优化方法可以使用并行加速,因此可以大大的加速计算速度。
基于随机梯度优化方法的思路为:找到一个简单的分布$q^(z) \in Q$来近似p(z|x), 目标$q^(z)$应该是$Q$中,与$p(z|x)$某种距离最小的那个。
为什么要用KL散步来度量两个分布的距离呢?
KL满足可导和凸性,使得它的计算更快;
我们没法通过上式求得$q^*(z)$,需要通过下面的转换把优化KL最小问题进行转换为求$q(z)$使得ELBO最大的问题.

这里的$log p(x)$是一个固定的常数。
平均场推断


